|
 |

|

М етоды анализа и прогноза.
За период исследования ледяного покрова Охотского моря был разработан ряд методов прогнозов и расчетов, используемых, в том числе, и в практике. К примеру, получены зависимости для прогноза ледовых явлений по отдельным районам моря, реализован физико-статистический метод прогноза средней и максимальной ледовитоси, основанный на учете состояния средней тропосферы над Восточной Сибирью в летний период и предзимье. Для фонового прогноза ледовитости предложен прогностический оператор в виде суперпозиции нескольких квазипериодических составляющих. Определенный вклад в решение поставленных задач внесла и попытка прогноза декадной ледовитости. Проведенные в последние годы в ДВНИГМИ исследования позволили обобщить существующие разработки и предложить методы прогноза комплекса ледовых параметров, определяющих ледовые условия в Охотском море. Помимо несомненных успехов, достигнутых при реализации физико-статистических моделей, определенные сдвиги получены также в области гидродинамического моделирования. Для Охотского моря была реализована гидродинамическая модель осенне-зимних процессов. Испытание модели показало хорошее качественное согласование модельных результатов с фактическими. В таблице 1 представлен список методов ледовых прогнозов и расчетов, разработанных для условий Охотского моря.
К наиболее перспективным методам прогнозирования ледовых условий, с учетом возможной реализации автоматизированной схемы прогноза в разрабатываемом в ДВНИГМИ АРМом-океанолога, следует отнести три последних из представленного списка.
Ф изико-статистические методы прогноза элементов ледового режима.
Характеристики, определяющие ледовые условия моря и формирующие ледовый режим, можно разделить на два типа:
1) одномерные (интегральные) - ледовитость, площадь зон различной сплоченности и т.д.;
2) многомерны (поля ледовых элементов) - сплоченность, возраст, формы льда и т. д.
При разработке методов прогнозов учитывались следующие предположения:
- ледовые условия предсказуемы;
- между ледовыми, атмосферными и гидросферными процессами существуют асинхронные связи.
Для решения задач прогнозирования была предложена и реализована автоматизированная физико-статистическая схема, включающая ряд этапов последовательного преобразования и отбора (этапы компрессии) привлекаемой информации, построения прогностического оператора и прогноз.
Модели для прогноза полей сплоченности, возраста, форм льда с заблаговременностью до трех декад и декадного положения кромок льда.
В качестве исходных данных для прогноза использовались:
- карты ледовых авмаразведок;
- карты приземного давления и геопотонциала Н500 над северным полушарием;
- сведения, поступающие из дальневосточных УГМС, содержащие данные о температуре воды и воздуха с прибрежных станций;
- в качестве дополнительной информации привлекались снимки ледяного покрова с ИСЗ.
Кромка льда представлялась положением ее характерных изгибов, фиксируемых лучами, выходящими из заранее выбранных реперных точек.
Поля ледовых элементов задавались по 50 сравнительно однородным районам, на которые разбивалось Охотское море.
Поля приземного давления и геопотециала Н500 снимались с синоптических карт по 50 точкам, расположенным в азиатско-американском секторе северного полушария, ограниченный меридианами 1000 в.д. - 1700 з.д. и параллелями 40-800 с.ш. Использовались средние декадные данные за период с ноября по май.
Температура воздуха снималась по 18 прибрежным станциям. Температура воды задавалась по 4 станциям, расположенных в районах основных проливов, соединяющих Охотское море с Тихим океаном и Японским морем.
На первом этапе все исходные поля преобразовывались посредством разложния по эмпирическим ортогональным функциям (Э.О.Ф.). В дальнейших преобразованиях участвовали коэффициенты разложения, отражающие наиболее крупномасштабные процессы и в сумме несущие около 90 % исходной информации.
Количество выбираемых коэффициентов разложения определялось формулой:
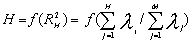 Где
Где 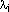 - собственные числа ковариационной матрицы рассматриваемого поля; М - общее количество собственных чисел (размерность поля); Н - выбираемая часть собственных векторов. - собственные числа ковариационной матрицы рассматриваемого поля; М - общее количество собственных чисел (размерность поля); Н - выбираемая часть собственных векторов.
На следующем этапе проводился отбор предикторов, коэффициенты корреляции которых с предиктантами превышали:
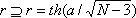 Где а - показатель уровня значимости отбираемых связей. Эта операция позволяет провести дальнейшее сокращение размерности вектора предиктора и уменьшить вероятность использования для прогноза случайных связей.
Где а - показатель уровня значимости отбираемых связей. Эта операция позволяет провести дальнейшее сокращение размерности вектора предиктора и уменьшить вероятность использования для прогноза случайных связей.
В связи с использованием множества полей предикторов предусмотрена возможность повторного разложения по Э.О.Ф.
При отсутствии связей, удовлетворяющих заданному уровню значимости, происходит автоматический переход к поиску предсказателей, удовлетворяющих менее строгим граничным критериям.
С помощью выбранных в результате многоэтапного преобразования предикторов строятся уравнения регрессии вида:
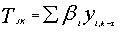 Где
Где  - отобранные предикторы; - отобранные предикторы; 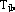 - коэффициенты разложения прогностического поля. - коэффициенты разложения прогностического поля.
Далее по спрогнозированным временным функциям проводится восстановления реального прогностического поля:
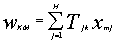 Здесь
Здесь 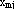 - собственные векторы разложения полей ледовых элементов. - собственные векторы разложения полей ледовых элементов.
После этого рассчитываются оценки прогноза: коэффициенты множественной корреляции, средние квадратические ошибки прогноза, обеспеченность и т.д.
В модели реализуется прогноз коэффициентов разложения с последующим восстановлением фактического поля, поэтому в качестве обобщенной оценки успешности вместо множественных коэффициентов корреляции используется свободный коэффициент корреляции К, показывающий уровень аппроксимации совокупности коэффициентов разложения, т. е. практически самого фактического поля:
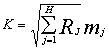 Где
Где 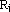 - коэффициент множественной корреляции для j-й временной функции; mj - относительная доля вклада j-й составляющей в суммарную изменчивость ледового элемента, определяемую H отобранными на этапе разложения функциями. - коэффициент множественной корреляции для j-й временной функции; mj - относительная доля вклада j-й составляющей в суммарную изменчивость ледового элемента, определяемую H отобранными на этапе разложения функциями.
Оперативные испытания модели показали весьма обнадеживающие результаты. В целом оправдываемость метода при прогнозе полей ледовых элементов с трехдекадной заблаговременностью превышает 70 %. Максимальная эффективность наблюдается при прогнозе положения кромки льда - 26%, сплоченности льда - 17% с заблаговременностью 1 декада, а с заблаговременностью 3 декады - 13 и 6 % соответственно. Эффективность прогноза возраста и форм льда несколько ниже. Сравнительный анализ результатов физико-статистического, инерционного и климатологического методов показал несомненное преимущество первого (таблица 2).
В настоящее время (начиная с зимы 1983-84 гг) метод прогноза положения кромки льда с заблаговременностью до 3-х декад используется в оперативной практике Приморского УГМС.
Модель для прогноза ледовитости Охотского моря на сезон.
В дополнение к исходным данным, рассмотренным выше, использовались индексы Белинского, характеризующие основные циркуляционные процессы над азиатско-американским сектором. Данные выбирались по ряду стандартных районов за период с августа по ноябрь.
Алгоритм прогноза ледовитости Охотского моря представлен схемой с трехкратной компрессией информации и последующей оценкой параметров. Выборки для построения прогностических уравнений формируются из информационного архива, записанного на технические носители.
Способ получения предикторов аналогичен предыдущей модели. Отобранные предикторы используются при построении уравнения регрессии вида:
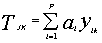 Где yik - отобранные на третьем этапе компрессии предикторы; P - их количество; Tjk - прогнозируемые коэффициенты разложения.
Где yik - отобранные на третьем этапе компрессии предикторы; P - их количество; Tjk - прогнозируемые коэффициенты разложения.
Сводный коэффициент корреляции P при прогнозе отобранных временных функциях разложения ледовитости, рассчитанный как средний за период авторских испытаний оказался равным 0.76, что относит полученные зависимости к категории хороших.
Фактическое распределение ледовитости восстанавливается по формуле:
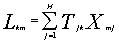 Где Н - количество отобранных на первом этапе коэффициентов разложения; xmj - собственные вектора этого разложения.
Где Н - количество отобранных на первом этапе коэффициентов разложения; xmj - собственные вектора этого разложения.
После этого рассчитываются оценки прогноза.
Схема прогноза полностью автоматизирована и при задании входных условий выдает прогностические рекомендации. Данная методика проверялась на независимом материале. Средняя оправдываемость прогнозов составила: без корректировки на вторую половину сезона - 65 %, с корректировкой - 81%. Соответственно средние оценки климатологического и инерционного методов составляют 47 и 45 %.
С 1983 г. данный метод внедрен в оперативную практику Приморского УГМС.
Долгосрочный прогноз ледовитости.
Принимается, что долгосрочные флюктуации ледовитости определяются крупномасштабными атмосферными процессами северного полушария. Наиболее общими показателями этих процессов являются характеристики центров действия атмосферы. Однако конкретный механизм влияния центров действия атмосферы в настоящий момент пока не выявлен, и возможную совокупность связей приходится представлять в виде статистических зависимостей.
В качестве исходной информации для долгосрочного прогноза ледовитости использовались:
1) карты ледовых авиаразведок;
2) средние месячные аномалии температуры в центрах действия атмосферы. Используется алеутская депрессия, азиатский зимний антициклон, канадский антициклон, охотский антициклон, летняя дальневосточная депрессия, северо-американский летний циклон, арктический антициклон, среднеазиатская депрессия;
3) индексы атмосферной циркуляции Вангенгейма, Ильинского, Каца.
Архив информации, содержащий данные о предиктантах и предикторах, с помощью генератора случайных чисел разбивается по заданному соотношению на две выборки - обучающую и проверочную. На обучающей выборке методом наименьших квадратов строятся два ряда частных описаний предиктанта последовательно для каждого предиктора:
- ряд степенных полиномов
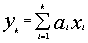
- ряд по тригонометрическим функциям
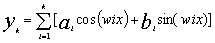
В качестве полинома оптимальной сложности каждого предиктора отбирались зависимости, минимизирующие на проверочной последовательности среднюю квадратическую ошибку прогноза.
При переборе трендов в список кандидатов в переменные первым номером всегда включалось время. После этого рассчитываются обобщенные функции от полученных на предшествующем этапе полиномов:
y = f(aj, yj)
В целях сокращения вычислительных процедур эта функция представлялась только в виде некоторого степенного полинома:
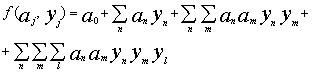 Затем последовательно отбрасываются по одному члену, имеющему минимальный коэффициент корреляции с предиктантом, и выбирается уравнение, минимизирующее на проверочной последовательности среднюю квадратическую ошибку прогноза.
Затем последовательно отбрасываются по одному члену, имеющему минимальный коэффициент корреляции с предиктантом, и выбирается уравнение, минимизирующее на проверочной последовательности среднюю квадратическую ошибку прогноза.
В силу недостаточного объема исходной информации количество одновременно анализируемых полиномов для последующего построения функции ограничивается пятью. При необходимости учета большего количества предикторов дополнительно используются частные описания вида:
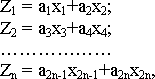
Где 2n - общее количество предикторов; а - коэффициенты уравнений, полученные методом наименьших квадратов; хn - рассчитанная оценка ошибки прогноза:
Z=y-f(aj,yj)
Для дальнейшего сжатия информации рассчитывается множественное уравнение регрессии, где в качестве предикторов выступают частные описания вида:
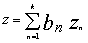
Результирующий прогноз получается как суперпозиция уравнений вида:
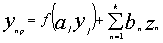
Отбор оптимального результирующего уравнения также происходит по материалам тестирования на проверочной выборке.
Результаты испытаний метода на проверочной последовательности показали среднюю оправдываемость прогноза по всему ледовому периоду около 80%.
Базируясь на приведенных оценках и учитывая, что климатологический метод дает оправдываемость около 60 %, а метод множественной линейной регрессии около 64 %, предложенную схему для долгосрочного прогноза ледовитости можно рекомендовать для практического использования.
Ч исленное моделирование ледяного покрова.
Разработка численных (гидро-термо-динамических) методов расчета гидрометеорологических элементов, по существу, являются гносеологическим моделированием, причем причинно-следственные зависимости в таких моделях описываются уравнениями гидротермодинамики.
В основе предложенной модели численного расчета (прогноза) параметров льда Охотского моря в осенне-зимний период лежат теоретические и практические разработки полученные в основном в ААНИИ. Модель получила дальнейшее развитие и усовершенствование с точки зрения приспособления ее к реальным физико-географическим особенностям Охотского моря и имеющейся гидрометеорологической информации. В частности, разработан метод расчета температуры воздуха с учетом трансформации воздушных масс по траекториям их перемещения над открытой акваторией моря. Учитывая особое значение турбулентных процессов и вертикальных движений в формирование структуры верхнего деятельного слоя Охотского моря, в модели разработан блок их расчета ниже слоя конвективного перемешивания.
Для получения предварительной качественной модели, на основе которой в последующем формировалась система уравнений, проведен анализ имеющейся гидрологической информации, что позволило:
- рассмотреть изменчивость гидрологической структуры верхнего деятельного слоя моря от месяца к месяцу в предзимний период ;
- выявить влияние гидрологических факторов на характерные особенности ледяного покрова.
Проведенный ряд экспериментальных расчетов по разработанной модели впервые позволил:
- представить картину осенне-зимних процессов на всей акватории Охотского моря во взаимосвязи с определяющими их гидрометеорологическими характеристиками;
- получить количественные значения изменчивости гидрологических элементов, в том числе глубины конвективного перемешивания и теплозапаса вод;
- рассчитать поле температуры воздуха и теплообмен на поверхности моря;
- оценить влияние различных факторов на ледяной покров и в первую очередь оценить роль гидрологической структуры вод верхнего деятельного слоя в формировании наиболее характерных особенностей ледяного покрова Охотского моря.
Численная модель.
В основе модели лежат уравнения баланса тепла и соли с учетом адвекции:
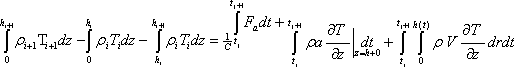
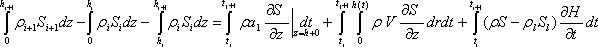
где С и  - теплоемкость и плотность воды; - теплоемкость и плотность воды;  l и Н - плотность и толщина льда; V - скорость течения по направлению r; а и а1 - коэффициенты вертикального турбулентного обмена в воде ниже однородного слоя; S и Sl - соленость воды и льда; t - время; h - толщина верхнего однородного слоя; i и i+1 - индексы, относящиеся к начальному (i) и последующему (i+1) моментам времени. l и Н - плотность и толщина льда; V - скорость течения по направлению r; а и а1 - коэффициенты вертикального турбулентного обмена в воде ниже однородного слоя; S и Sl - соленость воды и льда; t - время; h - толщина верхнего однородного слоя; i и i+1 - индексы, относящиеся к начальному (i) и последующему (i+1) моментам времени.
Fa - поток тепла от подстилающей поверхности к атмосфере определяется из уравнения баланса тепла:
Fa= Ft+Fu+(1-A)R+Q,
где Ft - турбулентный теплообмен; Fu - теплообмен за счет испарения; A - альбедо подстилающей поверхности; R - суммарная радиация; Q - эффективное излучение подстилающей поверхности.
Основой схемы расчета глубины однородного слоя является соотношение:
 h h   Расчет потоков тепла и соли к гомогенному слою производится по известным T, S - профилям при постоянном коэффициенте турбулентного обмена. Ниже слоя конвекции учитывается процесс диффузии:
Расчет потоков тепла и соли к гомогенному слою производится по известным T, S - профилям при постоянном коэффициенте турбулентного обмена. Ниже слоя конвекции учитывается процесс диффузии:

Расчет толщины льда производился по формуле:
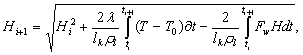
где Hi и Hi+1 - толщина льда на моменты времени ti и ti+1;  - теплопроводность морского льда; lk - теплота кристаллизации; T и T0 - температура на верхней и нижней поверхностях льда; Fw - поток тепла к нижней поверхности льда из воды; - теплопроводность морского льда; lk - теплота кристаллизации; T и T0 - температура на верхней и нижней поверхностях льда; Fw - поток тепла к нижней поверхности льда из воды;  - плотность льда. - плотность льда.
Расчет изменение плотности однородного слоя производится с учетом солености образующегося льда. Соленость льда рассчитывалась по формуле:
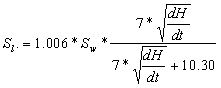
В результате моделирования получены характеристики не только самого ледяного покрова, но и ряд параметров, характеризующих гидрологические и метеорологические процессы, происходящие в осенне-зимний период: параметры конвективного перемешивания -температуру, соленость, глубину проникновения; тепловой баланс на поверхности моря, распределение температуры воздуха и так далее.
|
 | |